Scoperta una nuova classe di forme senza angoli per riempire lo spazio tridimensionale senza vuoti
Non solo angoli acuti o convessi, triangoli, quadrati ed esagoni. Non solo cubi e altri poliedri dello spazio tridimensionale.
La natura disegna anche altre forme e la matematica, ora, è in grado di leggerle, dando un nome e codificando queste “nuove” figure in grado di riempire lo spazio volumetrico riducendo al minimo gli angoli acuti.
Si chiamano “celle morbide” e, se ancora non le conosciamo, in realtà nella nostra quotidianità vi ci siamo trovati davanti tutti almeno una volta della vita, senza saperlo.
Quella che tecnicamente è definita come l’applicazione di modelli di riempimento dello spazio attraverso forme ripetute non sovrapposte è infatti il modo usato, per esempio, per rivestire un bagno utilizzando piastrelle di eguali dimensioni. Tecniche che l’uomo ha iniziato a sviluppare oltre 10 mila anni fa, con l’avvento delle prime pareti in muratura.
Dalla codifica all’algoritmo
Riguardo ai problemi legati a come eseguire le tassellature senza vuoti, la prima teoria geometrica risale a Platone.
La svolta, rispetto alle soluzioni classiche, arriva ora con un un team di matematici ungheresi che ha evidenziato come la piastrellatura con celle morbide sia possibile quando alcuni angoli vengono deformati in forme a cuspide, con angoli interni pari a zero.
I bordi di queste forme si incontrano tangenzialmente come in una lacrima, adattandosi perfettamente agli angoli arrotondati senza lasciare spazi vuoti.
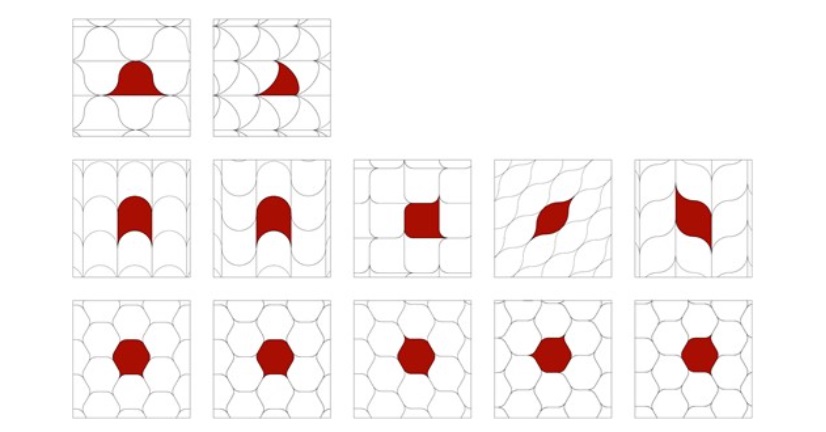“Stabilire e mantenere angoli acuti nelle cellule fisiche – sottolinea il lavoro pubblicato su Pnas Nexus – è difficile poiché la tensione superficiale e l’elasticità tendono naturalmente a smussare gli angoli”.
Così Gabor Domokos della Budapest University of Technology and Economics e i suoi colleghi hanno elaborato un algoritmo per convertire senza problemi le piastrelle poligonali o poliedriche in celle morbide.
La nuova forma in natura
La nuova forma, in realtà, in natura ha molteplici esempi in strutture biologiche che si sono evolute, per riempire lo spazio, cercando di limitare i vincoli nella loro crescita: dalle cipolle, alle cellule del sangue che viaggiano attraverso i capillari ad alta velocità, dal modo in cui i semi si compattano nelle piante ai processi di crescita della punta, fino alla conchiglia a spirale del nautilus, vero punto di svolta del lavoro.
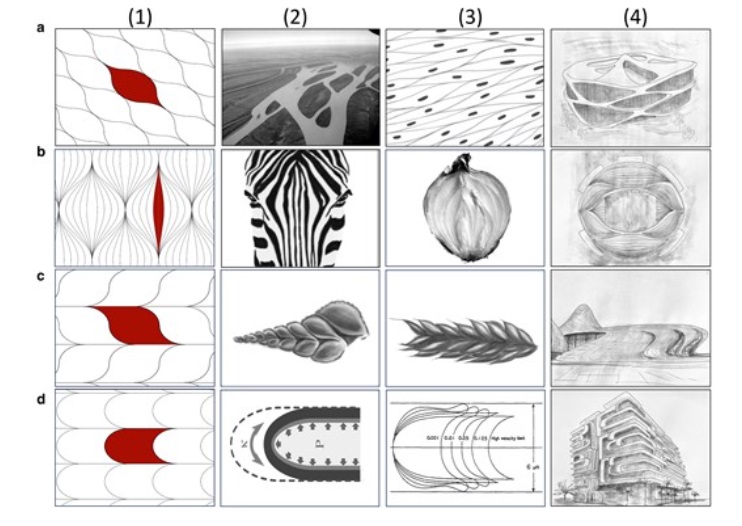
Nella loro trasfigurazione su piano, in 2D, le opzioni di queste forme sono piuttosto limitate: tutte le tessere devono avere almeno due angoli a cuspide.
“Ma in 3D – si legge nello studio – l’introduzione della morbidezza ha in serbo alcune sorprese. In particolare, queste celle morbide possono riempire lo spazio volumetrico senza avere alcun angolo“.
Le applicazioni
Lo studio cita anche esempi di celle morbide 2D che compaiono nelle opere architettoniche di Zaha Hadid o in quelle artistiche di Katsushika Hokusai e Victor Vasarely. Come riporta la rivista Nature, Domokos ipotizza che una piastrellatura morbida, nei materiali reali, consentirà di massimizzare una certa quantità fisica correlata, per esempio, all’energia di flessione nei bordi o alla tensione interfacciale.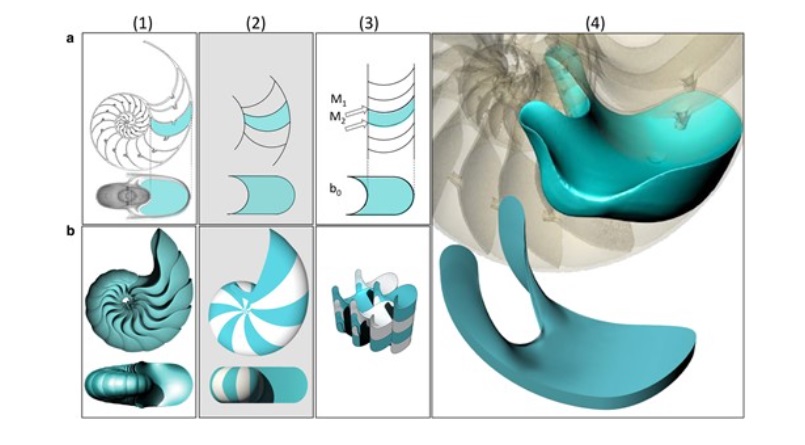
In collaborazione con gli architetti del California College of Arts di San Francisco, una volta completato il documento, il matematico ungherese e il coautore Alain Goriely dell’Università di Oxford hanno intanto già ideato una struttura utilizzando elementi a celle morbide realizzati impiegando in maniera opportuna una serie di gusci d’uovo.
